然而,只需使用2片廉价的集成电路就可以把幅度不恒定的PWM输出转换成精密的PWM输出电压。
1 电路原理
使用三端精密基准电源和模拟开关得到电压精密的PWM脉冲的电路原理如图1所示。D1为TL431三端基准电压集成电路,U1采用单刀双掷的模拟开关MAX4544;电阻R1、R2、R3根据具体的需要而定。当然,也可以采用其它型号的集成电路。

图1
当PWM脉冲为高电平(逻辑1)时,U1的COM端掷向常闭端(NC),TL431的调整脚与正电压脚相连,输出电压值为2.5 V。当PWM脉冲为低电平(逻辑0)时,U1的COM端掷向常开端(NO),TL431的输出电压经过R2、R3 分压后送到调整脚,此时输出电压值等于[(R2+R3)/R3]×2.5 V。本例中输出电压等于8 V。这样,当U1的IN 脚输入PWM信号时,电路相应地输出高电平为8 V,低电平为 2.5 V的PWM脉冲,其振幅为 8 V - 2.5 V = 5.5 V 。如果需要输出低电平为零的PWM信号,则再加上1个差分放大器就可解决。
在对于精密度的要求不是很高的场合,可以采用更简单的方法。图2为使用精密稳压二极管对PWM脉冲进行稳压限幅的电路图。在图2中,PWM信号经过高速运算放大器U1放大成为±12 V的输出电压,在经过R1的限流和D1的稳压后,得到 ±6.5 V 的PWM脉冲输出。
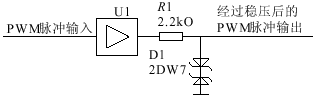
图2
2 误差分析
图1中,只要基准电源选取恰当,基准电源本身的误差完全可以忽略。除此之外,误差的来源主要有以下几个方面:
(1) 模拟开关的导通电阻引起的误差
模拟开关导通时有一定的导通电阻。TL431调整脚输入电流通过模拟开关时就会形成电压降,产生误差。MAX4544的导通电阻为35 Ω,而TL431的调整脚输入电流则在4 μA以下。由此而导致基准电压的误差小于140 μV,为2.5 V的 0.000 056,相当于二进制14位的精度。
(2) 开关延迟时间引入的误差
开关延迟时间将会引起脉冲占空比的变化,从而导致PWM输出脉冲产生误差。MAX4544的导通时间为30 ns,关断时间为25 ns。计算可知,当PWM频率为10 kHz时,由此产生的误差最大为0.0003,相当于12位的精度。如果PWM的频率选得较低,则开关延迟时间的影响相应减小。例如选取1 kHz时,引入误差为0.000 03,相当于15位的精度。
上述两项中真正影响输出电源精度的是这些参数随温度和时间的漂移。由于这两项参数本身的绝对值非常小,可以推知它们的漂移更小。
从以上的分析可知,由于附加电路引入的误差完全能够满足PWM的精度需求。
图2电路中,引起误差的原因主要有3个方面:
(1) 稳压二极管的动态电阻引入的误差
稳压二极管的动态电阻比较大,一般在几十Ω左右(工作电流5~10 mA时);而运算放大器的驱动能力比较小,只能使稳压二极管工作在较小的工作电流下。另外,稳压二极管小电流工作时的动态电阻更大,更容易引起电压变化。
(2) 稳压二极管温度漂移引入的误差
2DW7(2DW230~236)内部结构可以认为是2个稳压二极管对接串联而成的。其中一个二极管的正向电压降(具有负温度系数)对另一个稳压二极管的温度漂移(具有正温度系数)进行补偿,得到很低的温度系数。然而,当2DW7反向应用时,其温度漂移就不能得到恰当的补偿,从而导致负脉冲部分的温度系数较高。
(3) 运算放大器引入的误差
运算放大器的输入失调电压的漂移可直接导致脉冲振幅的误差;而转换速率(SR)过低,将导致脉冲方波波形的失真,继而引起电压的误差。失调电压温度漂移低并且转换速率高的运算放大器的价格将会很高。
但是,对于8~10位的PWM而言,该电路已经能够满足要求。对于要求更低的场合,可以用2个廉价的稳压二极管对接来代替2DW7。
3 应用实例
利用单片机的PWM输出,在图1的基础上增加RC滤波电路和1级运算放大器,得到0~10 V直流输出电压,作为变频器的控制信号,取得了良好的效果。图 3 所示为使用PWM输出控制变频器的实例。
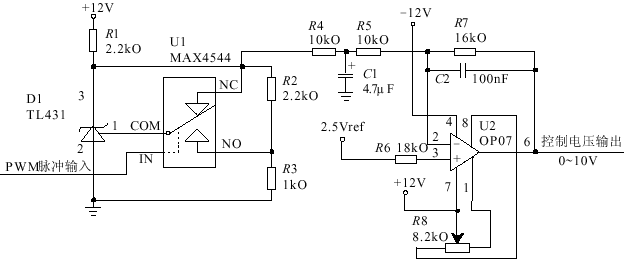
图3
*博客内容为网友个人发布,仅代表博主个人观点,如有侵权请联系工作人员删除。